Hello there. To solve this question, we have to interpret the question, draw the geometrical figure that represents the problem and solve for the measure of a segment using sines or cosines.
In this case, consider first the lake:
Now, draw a perpendicular line from one shore to another:
Consider you also have a straight line on the other shore, such that you can determine the angle from which you're rowing the boat.
Making a segment from one shore to another, this time 4 miles away from the first point, we get
In this case, the question asks you how far would you have to row.
For this, you need to determine the measure of the hypotenuse of the triangle.
Considering we have the measure of the opposite side to the angle, we might use the sine function that will give us:
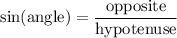
Plugging angle = 35º, opposite = 4, we want to determine hypotenuse.
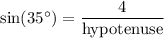
Cross multiply the values
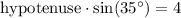
Divide both sides of the equation by a factor of sin(35º)
![\text{hypotenuse}=\frac{4}{\sin(35^(\circ))]()
Using a calculator, we get that
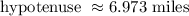
That we can round to the nearest integer as
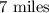
This is the answer to this question.