Question

A big cylinder of mass 5.25-kg is released from rest and rolls without slipping down an inclinedplane inclined at 18° to the horizontal. How fast is it moving after it has rolled 2.2m down theplane?O None of the aboveO2.6 m/s298.0 cm/s4.3 m/s5.2 m/s

Answer 1

First, if we sketch the situation, we have the following:

We'll use the energy approach to solve the problem. We need to find out the displacement in the y axis. This can be achieved by finding the opposing catete, which is

`y=2.2*sin(18°)=0.68m`

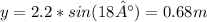
This is how much it has traveled in the y axis. Its initial energy (gravitational potential) can be written as:

`E=mgh=5.25*9.8*0.68=34.986J`

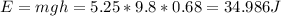
By the end, this same energy will have been turned into kinetic energy, thus:

`34.986=(mv^2)/(2)=(5.25*v^2)/(2)`

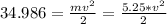
So we know that

`v^2=(2*34.986)/(5.25)`

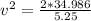
And finally

`v=\sqrt[\placeholder{⬚}]{(2*34.986)/(5.25)}=3.65(m)/(s)`

Then, our final answer is 3.65m/s