Question

Are these two lines parallel perpendicular or neither -3x+y=8, x+3y=7

Answer 1

Given:

The lines are:

`\begin{gathered} -3x+y=8\ldots\ldots\ldots\ldots\ldots\text{.}\mathrm{}(1) \\ x+3y=7\ldots\ldots..\ldots\ldots\ldots\text{.}(2) \end{gathered}`

To check whether the lines are parallel, perpendicular or neither.

To check this, we find the slopes of both lines and then check if the slopes are same then the lines are parallel, if the slopes are negavtive reciprocal of each other then the lines are perpendicular.

Standard form of line is y= mx +c

Standard form of line (1):

`\begin{gathered} -3x+y=8 \\ y=3x+8 \end{gathered}`

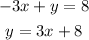
Slope of line (1) is 3

Now standard form of second line (2):

`\begin{gathered} x+3y=7 \\ 3y=-x+7 \\ y=-(x)/(3)+(7)/(3) \end{gathered}`

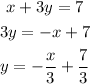
Slope of line (2) is -1/3

Now, the slopes 3 and -1/3 are negative reciprocal to each other.

Since,

`3*-(1)/(3)=-1`

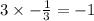
So, the given lines are perpendicular to each other.