To determine the surface area of the prism, you have to determine the area of each rectangular face of the prism and then add all areas.
The prism has 3 sets of equal faces:
Two are 40mm x 8mm rectangles
Two are 40mmx5mm rectangles
Two are 8mmx5mm rectangles
The area of any rectangle can be calculated as the product of its length and width, so that:
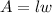
1) Area of 40x8 rectangles:
![\begin{gathered} A_1=40\cdot8=320\operatorname{mm} \\ 2A_1=640\operatorname{mm}^2 \end{gathered}]()
2) Area of the 40x5 rectangles
![\begin{gathered} A_2=40\cdot5=200\operatorname{mm}^2 \\ 2A_2=2\cdot200=400\operatorname{mm}^2 \end{gathered}]()
3) Area of the 8x5 rectangles:
![\begin{gathered} A_3=8\cdot5=40\operatorname{mm}^2 \\ 2A_3=2\cdot40=80\operatorname{mm}^2 \end{gathered}]()
Now you can determine the surface area of the rectangular prism:
![\begin{gathered} SA=2A_1+2A_2+2A_3 \\ SA=640+400+80 \\ SA=1120\operatorname{mm}^2 \end{gathered}]()
The surface area of the prism is 1120mm²