Given:
Frequency, f = 20 kHz.
Speed of sound in air, v = 331 m/s
Let's find the wavelength for the following:
• (a). When the temperature is 0 degrees Celsius.
To find the wavelength, apply the formula:
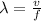
Where:
v is the speed
f is the frequency in Hz = 20 x 1000 = 20000 Hz.
To find the speed of sound on a day with 0 C, we have:
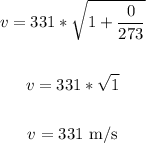
Now, to find the wavelength, input the values into the formula:
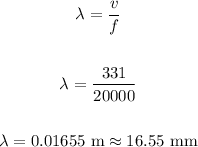
The wavelength when the temperature is 0 C is 16.55 mm.
• (b). Wavelength when the temperature is 40 degrees Celsius.
The speed, v, on a day when the temperature is 40 C will be:
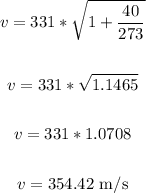
Hence, to find the wavelength, we have:
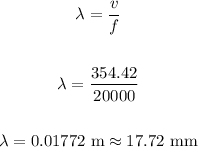
The wavelength on a day the temperature is 40 C is 17.72 mm.
ANSWER:
• (a). 16.55 mm
• (,b). 17.72 mm.