We need to find the mean and the median of the sets:

The mean of each set is found by adding all the values in the set and dividing the result by 10 (since there are 10 values in each set).
Thus, the mean, in minutes, for the set "Single line" is:
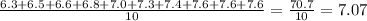
And the mean, in minutes, for the set "Individual lines" is:
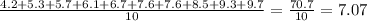
Now, the median of each set is the middle value of the sample. When there are two middle values (for even sample size), the median is the mean between those two values.
Since the sample sizes are even (10), the median, in minutes, for the set "Single line" is:
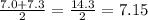
And the median, in minutes, for the set "Individual lines" is:
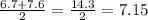
Now, notice that the mean (7.07) and the median (7.15) within each sample are not the same:
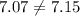
Thus, option B is wrong.
But the mean and median waiting times are the same between the two samples.
Therefore, the correct option is D.