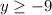Question

find the axis of symmetry, the max or min, y and x intercepts, the domain, and the range of y=(x+2)^2-9

Answer 1

`\begin{gathered} y=(x+2)^2-9 \\ y=(x+2)(x+2)-9 \\ y=x^2+2x+2x+4-9 \\ y=x^2+4x-5 \end{gathered}`

The quadratic equation is

`y=x^2+4x-5`

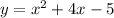
The solutions to the question can all be gotten from the graph of the quadratic equation;

The axis of symmetry is the point on the x-axis that divides the vertex of the parabola into two equal parts.

Therefore, the axis of symmetry occurs at x = -2

The graph curves downwards, hence it has a minimum point.

The minimum point occurs at y = -9

The y-intercept is the point where the curve cuts the y-axis when x = 0

Thus, the y-intercept occurs at y = -5

The x-intercept is the point where the curve cuts the x-axis at y = 0. The x-intercept also means the root of the equation

The x-intercept occurs at x = -5 and x = 1.

The domain of the equation is the set of all real values of x that will give real values for y.

Hence, the domain is from minus infinity to plus infinity. All real values of x satisfy the equation.

Domain =

`(-\infty,+\infty)`

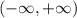
The range of a quadratic graph is the set of all real values of y that you can get by inputting real values of x

The graph ranges from y greater than or equal to -9

Therefore, the range is ;

`y\ge-9`