Question

A local restaurant has decided to rent a food truck for the Austin Kite Festival. The City Parks Department, who runs the festival charges $250 for any vendor. The restaurant must also rent a food truck for $300 that day. They are only planning to sell one item, a pulled pork plate. The cost for the restaurant is $1.50 for each plate made. They are planning on selling them for $9.50 each. a) write a cost function for this situation: b) write a revenue function for this situation. c) How many plates must they sell to break even?

Answer 1

The given information is:

- The festival charges $250 for any vendor

- The rent of the truck is $300

- The cost for each plate made is $1.50

- The value of the item is $9.50

Part A. The cost function for this situation is:

`\begin{gathered} Cost=fixed\text{ cost+cost of the plates} \\ C(x)=250+300+1.50x \\ C(x)=550+1.50x \end{gathered}`

Where x is the number of plates they made.

Part B. The revenue function is:

`R(x)=9.50x`

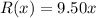
Where x is the number of plates they sell.

Part C. How many plates must they sell to break even?

We need to equal the cost to the revenue and solve for x:

`\begin{gathered} C(x)=R(x) \\ 550+1.50x=9.50x \\ 550=9.50x-1.50x \\ 550=x(9.50-1.50) \\ 550=x*8.00 \\ x=(550)/(8.00) \\ x=68.75 \\ x\approx69 \end{gathered}`

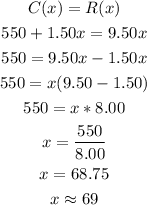
They must sell 69 plates to break even.