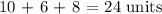Question

Find the perimeter of the triangle whose vertices are (-1,-6),(5,-6) and (5,2). Write exact answer. Do not round.

Answer 1

Step 1:

In this question, we are given the following:

Find the perimeter of the triangle whose vertices are (-1,-6),(5,-6), and (5,2).

Step 2:

The graph of the vertices of the triangle is as shown as below:

Now, let us find the lengths of the triangle,

First, ( -1, -6 ) and ( 5, 2 )

Second, ( -1,-6) and ( 5, -6)

Third, (5,2) and ( 5,-6)

Step 3:

Distance of ( -1, -6 ) and ( 5, 2) is calculated as follows:

`\begin{gathered} d\text{ = }\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ \text{d =}\sqrt[]{(5--1)^2+(2--6)^2} \\ d=\sqrt[]{(6)^2+(8)^2} \\ \text{d =}\sqrt[]{36+64} \\ \text{d =}\sqrt[]{100} \\ \text{d = 10} \end{gathered}`

Distance of ( -1,-6) and ( 5, -6) is calculated as follows:

`\begin{gathered} d\text{ =}\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ d\text{ = }\sqrt[]{(5--1)^2+(-6--6)^2} \\ d\text{ =}\sqrt[]{(6)^2+(0)^2_{}} \\ \text{d =}\sqrt[]{36} \\ d\text{ =6} \end{gathered}`

Distance of (5,2) and ( 5,-6) is calculated as follows:

`\begin{gathered} d\text{ =}\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ d\text{ =}\sqrt[]{(5-5)^2+(-6-2)^2} \\ \text{d =}\sqrt[]{(0)^2+(-8)^2} \\ d\text{ =}\sqrt[]{0+64} \\ \text{d =}\sqrt[]{64} \\ \text{d = 8} \end{gathered}`

CONCLUSION:

The perimeter of the triangle is:

`10\text{ + 6 + 8 = 24 units}`