The power reducing formula for the fourth power of the cosine function is:
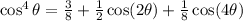
Replace θ=3x to find the expression for cos⁴(3x) in terms of the first power of the cosine function:
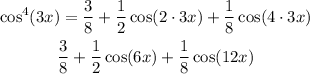
Therefore, the answer is:
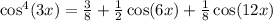
Use the second option to write this expression as input.