Question

Suppose triangle GEF is similar to triangle ABC.Point G Has coordinates (-1.75,1.75) and point E has coordinates(-1.75-5,25) Part A:What is the scale factor between the two triangles ? Part B: what are the coordinates of F? Part C : what is the relationship between areas of triangle ABC and triangle GEF ?

Answer 1

ΔGEF≅ΔABC

Point G (-1.75,1.75)

Point E (-1.75,-5.25)

Part A

To determine the scale factor first determine the coordinates of points A, B and C from the grid:

Point A(-1,1)

Point B(-1,-3)

Point C(6,-3)

The order of the letters when the triangles are named, indicate the position of the vertices and which ones are corresponding.

Triangle GEF will have the same shape as triangle ABC and vertices:

G corresponds to A

E corresponds to B

C corresponds to F

Knowing this you can compare the coordinates of two corresponding points to determine the scale factor. When the triangle was transformed, the coordinates were divided by the factor k to determine the new coordinates, following the rule:

Preimage → Image

P(x,y) → P'(x÷k,y÷k)

So to determine the scale factor you have to divide the original coordinate by the transformed ones:

For example using the x-coordinates of A and G:

`k=(-1)/(-1.75)=(4)/(7)`

The scale factor used is the same for both coordinates, this means that doing the same division over the y-coordinates of both points should give the same result:

`k=(1)/(1.75)=(4)/(7)`

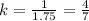
So, the scale factor used to create ΔGEF is k=4/7

Part B

To determine the coordinates of F, you have to divide the coordinates of its corresponding point of ABC by the scale factor.

C(6,-3)→F(6÷4/7,-3÷4/7)= F(10.5,-5.25)

Part C

ΔGEF is larger than ΔABC this indicates that it was dilated.

The are of ΔGEF is 4/7 times larger than the area of ΔABC