Question

A circle is inside a square The radius of the circle is decreasing at a rate of 4 meters per minute and the sides of the square are decreasing at a rate of 5 meters per minute. When the radius is 2 meters, and the sides are 24 meters, then how fast is the AREA outside the circle but inside the square changing ? The rate of change of the area enclosed between the circle and the square is square meters per minute.

Answer 1

see the figure below to better understand the problem

The area of the square is

`A=b^2`

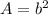
The area of the circle is given by

`A=\pi r^2`

The area outside the circle but inside the square is given by the equation

`A=b^2-\pi r^2`

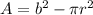
Find out dA/dt

using implicit differentiation

`(dA)/(dt)=2b(db)/(dt)-2\pi r(dr)/(dt)`

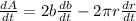
Remember that

we have

db/dt=-5 m/min

dr/dt=-4 m/min

substitute

`\begin{gathered} (dA)/(dt)=2b(-5)-2\pi r(-4) \\ \\ (dA)/(dt)=-10b+8\pi r \end{gathered}`

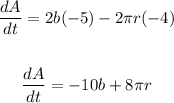
Evaluate for r=2 m and b=24 m

`\begin{gathered} (dA)/(dt)=-10(24)+8\pi(2) \\ \\ (dA)/(dt)=-240+16\pi \\ \\ (dA)/(dt)=-189.73\text{ }(m^2)/(min) \end{gathered}`

Round to the nearest whole number

the answer is -190 m2/min (negative because is decreasing)