Question

why does a projectile launched at 45 degrees goes further than any other angle at the same initial velocity.

Answer 1

Assuming that the air resistance on the projectile is negligible, and that the projectile is launched over a level surface.

Assume that the projectile is launched with an initial velocity of
`v_(0)` at
`\theta` (
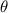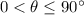`0 < \theta \le 90^(\circ)`) above the horizon. The range of this projectile would be
`({v_(0)}^(2)/g)\, \sin(2\, \theta)`.

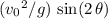For any given
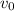`v_(0)\!`, this expression for the range is maximized when
`\theta = 45^(\circ)`.

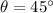Step-by-step explanation:

The range of a projectile is the horizontal displacement of the projectile between where it took off and where it landed.

If the initial velocity of this projectile is
`v_(0)` at an angle of
`\theta` (
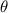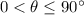`0 < \theta \le 90^(\circ)`) above the horizon:

• the vertical component of the initial velocity would be
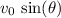  `v_(0)\, \sin(\theta)`, and
• the horizontal component of the initial velocity would be
  `v_(0)\, \cos(\theta)`.

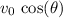Assuming that the air resistance on the projectile is negligible. Let
`g` denote the gravitational field strength. The projectile would accelerate downwards with an acceleration of
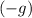`(-g)` during the entire flight.

If the projectile is launched over level ground (i.e., not from the top of a hill,) the projectile would land with a vertical velocity of
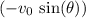`(-v_(0)\, \sin(\theta))`. In other words, right before the projectile lands, the vertical velocity would have the same magnitude as the initial value, but would be in an opposite direction.

The change to the vertical velocity of the projectile would be
`(-v_(0)\, \sin(\theta)) - (v_(0)\, \sin(\theta)) = -2\, v_(0)\, \sin(\theta)`.

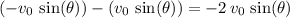Since acceleration is constant, the duration of the flight could be found by dividing the change in velocity by the acceleration. Thus, the projectile would have travelled for a duration of
`(-2\, v_(0)\, \sin(\theta)) / (-g) = 2\, v_(0)\, \sin(\theta)`.

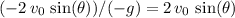At a horizontal velocity of
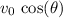`v_(0)\, \cos(\theta)`, that duration would allow the projectile to cover a range of:

`\begin{aligned}& \left((2\, v_(0)\, \sin(\theta))/(g)\right)\, (v_(0)\, \cos(\theta)) \\ =\; & \frac{{v_(0)}^(2)}{g}\, (2\, \sin(\theta)\, \cos(\theta)) \end{aligned}`.

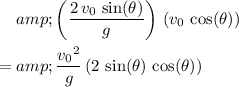By the double-angle identity of sine,
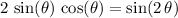`2\, \sin(\theta)\, \cos(\theta) = \sin(2\, \theta)`. Thus, the expression for the range of this projectile would be equivalent to:

`\begin{aligned}& \frac{{v_(0)}^(2)}{g}\, (2\, \sin(\theta)\, \cos(\theta)) \\ =\; & \frac{{v_(0)}^(2)}{g}\, (\sin(2\, \theta))\end{aligned}`.

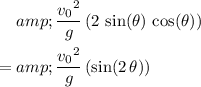Over the range of
`0 < \theta \le 90^(\circ)`,
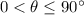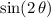`\sin(2\, \theta)` would be maximized when
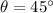`\theta = 45^(\circ)`, where
`\sin(2\, \theta) = \sin(90^(\circ)) = 1`.

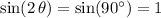Thus, for any given initial velocity
`v_(0)`, the range of the projectile over level ground would be maximized if
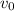`v_(0)\!` is at an angle of
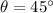`\theta = 45^(\circ)` above the horizon.