Question

Solve the following system algebraically. I need this done ASAP

Answer 1

We have to solve the system of equations:

`\begin{gathered} 2x+3y=-10 \\ 5x+2y=8 \end{gathered}`

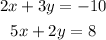
We can solve it by substitution.

We find the value of x in function of y from the first equation:

`\begin{gathered} 2x+3y=-10 \\ 2x=-10-3y \\ x=(-10-3y)/(2) \end{gathered}`

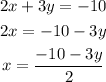
Then, we substitute the value of x in the second equation and solve for y:

`\begin{gathered} 5x+2y=8 \\ 5((-10-3y)/(2))+2y=8 \\ -(5\cdot10)/(2)-(5\cdot3y)/(2)+2y=8 \\ -25-(15)/(2)y+2y=8 \\ (2-(15)/(2))y=8+25 \\ (4-15)/(2)y=33 \\ (-11)/(2)y=33 \\ y=(33\cdot2)/(-11) \\ y=-(66)/(11) \\ y=-6 \end{gathered}`

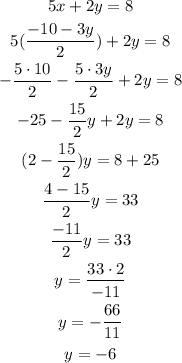
With the value of y=-6, we can solve for x:

`x=(-10-3y)/(2)=(-10-3\cdot(-6))/(2)=(-10+18)/(2)=(8)/(2)=4`

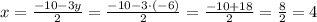
Answer: x=4 and y=-6