Question

Find the probability of selecting a 10 or diamond when a card is drawn from a standard deck of cards.

Answer 1

The probability of selecting a 10 or Diamond when a card is drawn from a standard deck of cards is: 17/52

The question asks us to find the probability of picking a 10 or diamond from a deck of cards.

A standard deck of cards contains 52 cards in total.

The deck contains 4 "10s"

And the deck also contains 13 diamond cards.

Thus, we can find the probability of drawing a "10" as:

`P(10)=\frac{n\text{umber of 10s}}{total\text{ number of cards in deck}}=(4)/(52)`

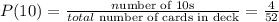
Similarly, we can find the probability of drawing a diamond as:

`P(\text{diamond)}=\frac{n\text{umber of diamonds}}{total\text{ number of cards in deck}}=(13)/(52)`

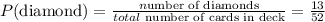
Now that we have the individual probabilities, we can find the probability of drawing a 10 or a diamond using the OR probability:

`\begin{gathered} P(A\text{ OR B)= P(A) + P(B)} \\ \text{where, A and B are independent events} \end{gathered}`

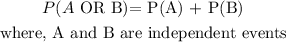
Therefore, we can solve the question. This is done below:

`\begin{gathered} \text{Probability of selecting a 10 or a diamond P(10 OR Diamond)=} \\ P(10)+P(\text{Diamond)} \\ \\ \text{But P(10)=}(4)/(52) \\ P(\text{Diamond)}=(13)/(52) \\ \\ \therefore P(10\text{ OR Diamond)=}(4)/(52)+(13)/(52)=(17)/(52) \end{gathered}`

Thus, the probability of selecting a 10 or Diamond when a card is drawn from a standard deck of cards is: 17/52