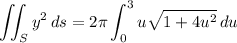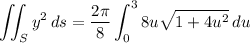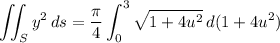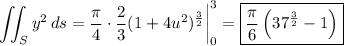Question

Evaluate the surface integral. S y2 ds s is the part of the sphere x2 + y2 + z2 = 36 that lies inside the cylinder x2 + y2 = 9 and above the xy-plane.

Answer 1

Parameterize S in cylindrical coordinates by the vector function

r(u, v) = (x(u, v), y(u, v), z(u, v))

with

x(u, v) = u cos(v)

y(u, v) = u sin(v)

z(u, v) = 36 - u²

with 0 ≤ u ≤ 3 and 0 ≤ v ≤ 2π. Take the normal vector to S to be

`\vec n = (\partial r)/(\partial u) * (\partial r)/(\partial v) = (2u^2\cos(v),2u^2\sin(v),u)`

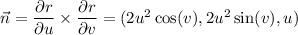
so that the surface element is

`dS = \|\vec n\| \, du\,dv = u √(1+4u^2)\, du\, dv`

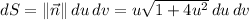
Then the surface integral is

`\displaystyle \iint_S y^2\,ds = \int_0^(2\pi) \int_0^3 u√(1+4u^2) \, du\, dv`

`\displaystyle \iint_S y^2\,ds = 2\pi \int_0^3 u√(1+4u^2) \, du`

`\displaystyle \iint_S y^2\,ds = \frac{2\pi}8 \int_0^3 8u√(1+4u^2) \, du`

`\displaystyle \iint_S y^2\,ds = \frac\pi4 \int_0^3 √(1+4u^2) \, d(1+4u^2)`

`\displaystyle \iint_S y^2\,ds = \frac\pi4 \cdot \frac23(1+4u^2)^(\frac32) \bigg|_0^3 = \boxed{\frac\pi6 \left(37^(\frac32)-1\right)}`