To answer this question, first we need to properly understand the definition of median and mean, and also understand what it means to be "roughly symmetrical".
Let's start with the definition of median.
"the median is the value separating the higher half from the lower half of a data sample"
If we have an odd amount of elements in our dataset, the median is literally the middle element of our set.
Example:
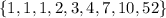
We have four elements below 3, and four elements above 3, therefore, the median of this dataset is 3.
If we have an even amount of elements, the median is the mean between the two elements in the middle.
Example:
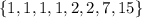
The elements in the middle are 1 and 2. This means our median is
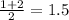
1.5.
Now, let's understand the mean.
By definition, The Arithmetic Mean is the average of the numbers: a calculated "central" value of a set of numbers, given by the sum of all elements divided by the amount of elements.
Examples:
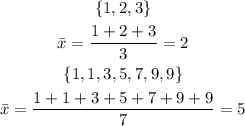
Now that we know what mean and median exactly are, let's try to understand what it means to be "roughly symmetrical".
When talking about histograms, Close to symmetric means the data are roughly the same in height and location on either side of the center of the histogram.
As the histogram gets closer to symmetric, the mean approaches the middle values, to be more specific, If the histogram is close to symmetric, then the mean and median are close to each other.
Since the statement says "roughly symmetrical" this is the only thing we can claim. If we have more values to the right in our roughly symmetrical distribution, the mean will be a little bit bigger than then median, and if we have more values to the left in our roughly symmetrical distribution, the mean will be a little bit smaller than then median.