Question

Use limit definition to find derivative of 4x^2 + 3x - 10

Answer 1

Given:

`f(x)=4x^2+3x-10.`

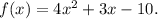
The formula to find the derivative of the function by using limit is

`f^(\prime)(x)=\lim _(h\to0)(f(x+h)-f(x))/(h)`

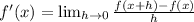
Replace x=x+h in the given function f(x) to find f(x+h).

`f(x+h_{})=4(x+h)^2+3(x+h)-10.`

`f(x+h_{})=4(x^2+2hx+h^2)+3x+3h-10.`

`f(x+h_{})=4x^2+8hx+4h^2+3x+3h-10.`

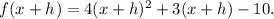
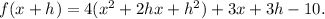
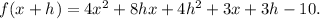
Substitute know values in the given formula, we get

`f^(\prime)(x)=\lim _(h\to0)((4x^2+8hx+4h^2+3x+3h-10)-(4x^2+3x-10))/(h)`

`f^(\prime)(x)=\lim _(h\to0)(4x^2+8hx+4h^2+3x+3h-10-4x^2-3x-10)/(h)`

`f^(\prime)(x)=\lim _(h\to0)(4x^2-4x^2+8hx+4h^2+3x-3x+3h-10-10)/(h)`

`f^(\prime)(x)=\lim _(h\to0)(8hx+4h^2+3h)/(h)`

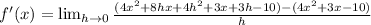
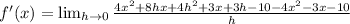
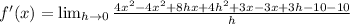
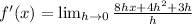
Taking out the common term h, we get

`f^(\prime)(x)=\lim _(h\to0)(h(8x+4h+3))/(h)`

`f^(\prime)(x)=\lim _(h\to0)(8x+4h+3)`

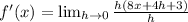
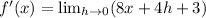
Taking limit, we get

`f^(\prime)(x)=8x+4(0)+3`

`f^(\prime)(x)=8x+3`

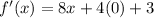
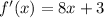
Hence the derivative of the given function is 8x+3.