a) The initial temperature of the liquid is simply the temperature of the liquid at time m = 0
Thus, we have the temperature to be:
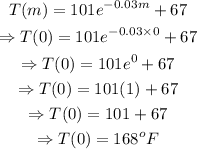
The initial temperature of the liquid is 168 degrees Fahrenheit
b) The time when the temperature of the liquid will reach 100 degrees Fahrenheit is obtained as follows:

Now, take the natural logarithm of both sides, as follows:
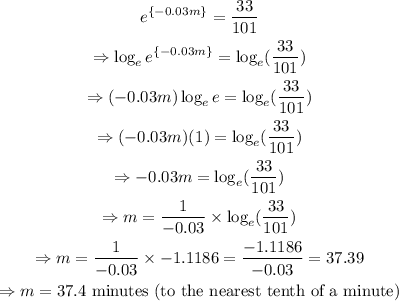
The time when the temperature of the liquid will reach 100 degrees Fahrenheit is 37.4 minutes