Explanation
We are given the following function:
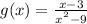
We are required to determine the limit of the function above as it approaches 3.
This is achieved as:
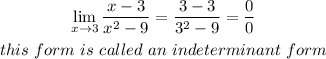
Since the method above cannot give an information on the limit, we need to try another method as follows:
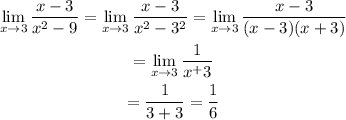
Hence, the answer is 1/6.