we know that
The area of complete circle subtends a central angle of 360 degrees
so
using proportion
Find out the area of the sector with a central angle of 45 degrees
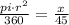
we have
r=8 units
substitute and solve for x
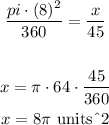
therefore
the answer is 8pi square units
option B