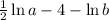The best way to find Arianna's errors is to attempt to work out the problem on our own.
We are given the expression
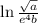
Her first step was correct, we should rewrite our radical as a fractional exponent.

However, in the next step, she should not have written the expression as two natural logs as a fraction. Instead, we have to apply the quotient property:
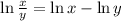
Instead, we will have
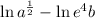
Arianna correctly rewrote the exponent of "a" as a coefficient, but not for "e". Before we get there, let's expand the second part of the expression using the product property:
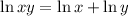
So, we will have

Applying the product property, Arianna should have moved the 4 to be a coefficient of ln(e):
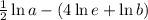
The rest of her work is fine, so let's just finish the expression from here. The identity property of natural states

so now we can have

And finally, we will distribute the negative:
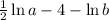
Part 2 a) Arianna had these two mistakes: First, she should have written the division as a subtraction. Second, she should have written the exponent 4 as a coefficient in front of ln(e) rather than ln(4e).
Part 2 b) the final expression should really be