Question

Simplify the complex rational expression. When typing your answer for the numerator and denominator be sure to type the term with the variable first with no spaces between characters. If an exponent is needed use the carrot key (^) by pressing shift and 6 at the same time.\frac{\left(\frac{2}{a}+\frac{7}{b}\right)}{b}The numerator is AnswerThe denominator is Answer

Answer 1

The given expression is

`(((2)/(a)+(7)/(b)))/(b)`

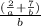
To add 2 fractions we have to give them the same denominators

In the up part (numerator) we have 2 different denominators a and b

Then the common denominator of the 2 fractions must be the product of them

`(2)/(a)+(7)/(b)=(2b)/(ab)+(7a)/(ab)=(2b+7a)/(ab)`

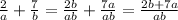
Then the fraction will be

`((2b+7a)/(ab))/(b)`

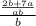
Now, we will multiply the denominator of up by the denominator of the first fraction (ab x b)

`((2b+7a)/(ab))/(b)=(2b+7a)/(b(ab))`

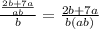
Multiply b by b to simplify, then

`(2b+7a)/(b(ab))=(2b+7a)/(ab^2)`

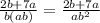
The numerator is 2b + 7a

The denominator is ab^2