In order to calculate the time needed, let's use the formula below:
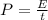
Where P is the power in Watts, E is the energy/work in Joules and t is the time in seconds.
First, let's convert the energy from kJ to J (1 kJ = 1000 J):
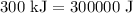
So, for P = 400, we have:
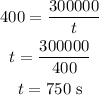
Therefore the time needed is 750 seconds.