Given,
The charge generated, q=0.0012 C
The energy of the Van der Graaf generator, E=1093 J
The time it takes for the generator to produce the given amount of charge, t=.005 s
The current is given by the time rate of the flow of charges. That is,
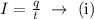
The voltage is calculated using the formula,
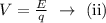
From Ohm's law, the voltage is given by,
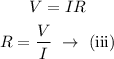
On substituting equation (i) and (ii) in equation (iii),
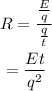
On substituting the known values,
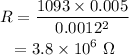
Thus the resistance of the air gap is 3.8×10⁶ Ω