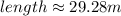Given that:
- The triangle is isosceles.
- Its base is 49.96 meters.
- Each base angle is 31.43°.
You can draw the triangle. See the picture shown below (it is not drawn the scale):
Notice that the Isosceles Triangle can be divided into two equal Right Triangles. Then, you know that:
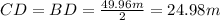
Since it is isosceles, the sides AB and AC have equal length.
Then, you can choose one of the equal Right Triangles and use the following Trigonometric Function in order to find the length of each equal side:
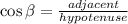
In this case, you can set up that:
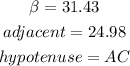
Therefore, substituting values and solving for AC, you get:
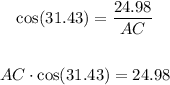
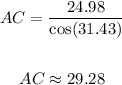
Hence, the answer is:
The length of the two equal sides of the triangle is: