The power consumed by the resistor can be expressed as,
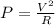
Substitute the given values,
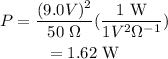
The thermal energy produced in the given time can be expressed as,
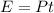
Plug in the known values,
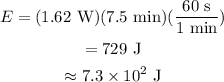
Thus, the thermal energy produced is 7.3*10^2 J which means fourth option is correct.