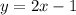Given:
There are given the points:
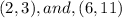
Step-by-step explanation:
According to the question:
We need to find the equation:
So,
To find the equation, first, we need to find the slope of the line:
So,
From the formula of slope:

Then,
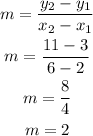
Now,
From the formula to find the equation of line:

Then,
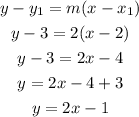
Final answer:;
Hence, the equation of the line is shown below: