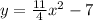Given:
The vertex of the parabola, (h, k) = (0, -7)
The parabola passes through the point (x, y) = (2,4).
To find the parabola equation:
The general form is,
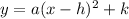
Substitute h=0, k=-7, x=2, and y=4. We get,
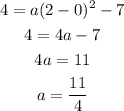
Substitute the values of a, h, and k in the general form.
We get,
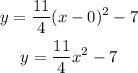
Hence, the parabola equation is,