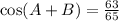Remember the following formula for the cosine of the sum of two angles:

On the other hand, from the Pythagorean Identity:
![\begin{gathered} \cos ^2(x)+\sin ^2(x)=1 \\ \Rightarrow\cos (x)=\sqrt[]{1-\sin ^2(x)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/v8hnny2zn6u2s3s2gnv19u0016egugdnqn.png)
The sign of the cosine of an angle is positive if that angle is in the first quadrant or the fourth quadrant. If it is in the second or third quadrant, the cosine will be negative.
Find the cosine of A and B using the Pythagorean Identity and find the sign of the cosine by checking the quadrant in which the angle is placed.
Since sin(A)=4/5 with A in the second quadrant, then:
![\begin{gathered} \cos (A)=-\sqrt[]{1-((4)/(5)})^2 \\ =-(3)/(5) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/m1kias0e1txqaf9i9bvyedxifufi9n4b3z.png)
Since sin(B)=-12/13 with B in the third quadrant, then:
![\begin{gathered} \cos (B)=-\sqrt[]{1-(-(12)/(13))^2} \\ =-(5)/(13) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/mn23ribmbuj4c2a86nzxbz88im0yjxv3sw.png)
Substitute the values for cos(A), cos(B), sin(A) and sin(B) into the formula to find the value of cos(A+B):
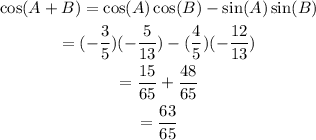
Therefore: