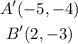Question

The vertices of the polygon shown have integral coordinates. The polygon will be rotated 180°about the origin and then reflected over the y-axis.76АNWB..7 -6 -5 4 3 2 1 1 2 3 4 5 6 7-4di u WNNoAfter these transformation:The coordinates of A' are (The coordinates of B' are (:: -6:: -5:: -3::-2:: -1:: 0:: 1:: 2:: 3:: 5.: 6

Answer 1

`\begin{gathered} A(-5,-4) \\ B^(\prime)(2,-3) \end{gathered}`

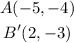
Step-by-step explanation

We want to find the coordinates of A' and B' after the transformations.

First, it was rotated 180 degrees about the origin.

When a point is rotated 180 degrees about the origin, its coordinates change as follows:

`(x,y)\to(-x,-y)`

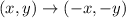
The coordinate of A and B are:

`\begin{gathered} A(-5,4) \\ B(2,3) \end{gathered}`

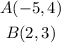
Therefore, they become:

`\begin{gathered} A(5,-4) \\ B(-2,-3) \end{gathered}`

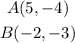
Then, the polygon was reflected over the y-axis.

When a point is reflected over the y-axis, its coordinates change as follows:

`(x,y)\to(-x,y)`

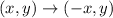
Therefore, after these transformations, the coordinates of A and B become:

`\begin{gathered} A^(\prime)(-5,-4) \\ B^(\prime)(2,-3) \end{gathered}`