Question

I have a home work due in 10 mins can you please help me out?

Answer 1

Use Coulomb's Law to find the electric force.

`F=K\cdot(q_1\cdot q_2)/((d_(12))^2)`

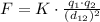
In this case, both particles have the same charge magnitude because both are elementary particles, however, they have opposite charge nature, a proton is positive and an electron is negative.

All the magnitudes we know are

`\begin{gathered} e=-1.60*10^(-19)C \\ p=+1.60*10^(-19)C \\ \text{Also,} \\ K=8.99*10^9\cdot(N\cdot m^2)/(C^2) \\ d_(12)=1.0*10^(-10)m \end{gathered}`

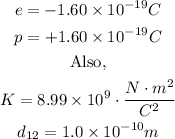
Use the magnitudes in the formula to find F.

`\begin{gathered} F=8.99*10^9\cdot(N\cdot m^2)/(C^2)\cdot(|-1.60*10^(-19)C|\cdot|+1.60*10^(-19)C|)/((1.0*10^(-10)m)^2) \\ F=(23.01*10^(9-19-19))/(1*10^(-20))N \\ F=(23.01*10^(-29))/(10^(-20))N \\ F=23.01*10^(-29+20)N \\ F=23.01*10^(-9)N \\ F=2.3*10^(-8)N \end{gathered}`

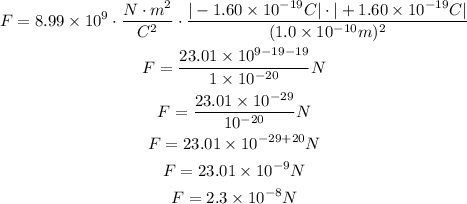
Therefore, the answer is B.