Question

without graphing, describe the transformation of each parabola or absolute value function y = 2 |x|+ 1

Answer 1

Remember the following transformations of a function:

`c\cdot f(x)`

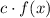
This transformation stretches the function over the vertical axis if c>1 and shrinks it if 0

If c is positive, the orientation is mantained, and if c is negative, the function is also flipped over (it shrinks if -1

`f(x)+c`

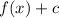
This transformation moves the function vertically c units. It goes up if c>0 and down if c<0.

Therefore, starting with the absolute value function:

`\lvert x\rvert`

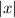
Multiply the function by 2:

`2\cdot\lvert x\rvert`

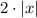
Since 2>1, then this is a vertical stretching by a factor of 2.

Next, add 1:

`2\cdot\lvert x\rvert+1`

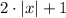
This will translate the stretched absolute value function one unit upwards.

Therefore, the complete description of the transfromation would be:

`y=2\cdot\lvert x\rvert+1`

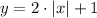
Is a vertical stretching of the absolute value function by a factor of 2, translated 1 unit upwards.