Given:
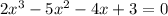
Required:
To check that 3 is a root of the given equation.
Step-by-step explanation:
Substitute x = 3 in the L.H.S. of the given equation.
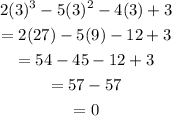
This is the R.H.S.
Thus x=3 is a root of the given equatio.
Final Answer:
x= 3 is a root of the given equatio.