Question

Help to write the quartic model for the number of phones sold in a given year.

Answer 1

`\begin{gathered} C)P(x)=-0.26x^4+7.62x^3-73.91x^2+296.58x+68.52 \\ Estimated\: number\: of\: phones\: sold\: in\: 2010\: is\: 663 \end{gathered}`

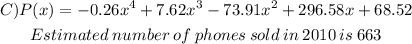
1) We were told to find a quartic model, so clearly we can focus on the 4th-degree polynomials.

2) Once we do that, let's test each of the entries and their outputs plugging into x the year:

`\begin{gathered} (3,478) \\ P(x)=-0.26x^4+7.62x^3-73.91x^2+296.58x+68.52 \\ P(3)=-0.26(3)^4+7.62(3)^3-73.91(3)^2+296.58(3)+68.52 \\ P(3)=477.75\approx478 \\ \end{gathered}`

Note that the first year is 2000, So, P(0) refers to 200, and P(3) refers to 2003.

Since we want to find an estimate for 2010 let's plug into that x=10

`\begin{gathered} P(10)=-0.26(10)^4+7.62(10)^3-73.91(10)^2+296.58(10)+68.52 \\ P(10)=663.32\approx663 \end{gathered}`

So, the answer is the third from top to bottom.