We need to solve the equation
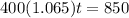
In order to do so, we can first divide both sides of the equation by 400:
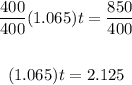
Now, to isolate the variable t on the left side and find its value, we can divide both sides by 1.065:

Therefore, rounding to two decimal places, the answer is 2.00.