Explanation:
Given the function:
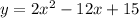
First, we find the vertex of the parabola.
Vertex
The equation of the axis of symmetry is calculated using the formula:
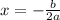
From the function: a=2, b=-12
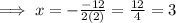
Substitute x=3 into y to find the y-coordinate at the vertex.
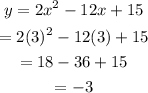
The vertex is at (3, -3).
Two points to the left of the vertex
When x=2
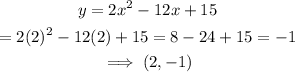
When x=1
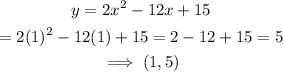
Two points to the right of the vertex
When x=4
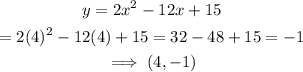
When x=5
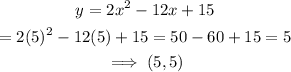
Answer:
Plot these points on the graph: (3, -3), (2,-1), (1,5), (4,-1), and (5,5).