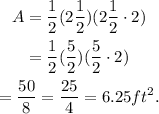To solve this problem, we will use the following formula for the area of a trapezoid:
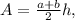
where a, and b are the lengths of the bases and h is the height.
Now, we are given that ( we will omit the units to simplify the calculations):
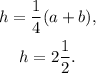
Therefore:
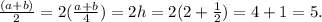
Substituting in the above formula, we get:
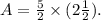
Simplifying the above result, we get:
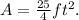
Answer: