Question

Situation: A .71-kg billiard ball moving at 2.5 m/s in the x-direction strikes a stationary ball of the same mass. After the collision, the first ball moves at 2.17 m/s, at an angle of 30.0° with respect to the original line of motion. Assuming an elastic collision (and ignoring friction and rotational motion), answer the following questions to find the struck ball's momentum after the collision.1. Calculate the x-component of the first ball's final momentum after the collision in kg*m/s.2. Using the conservation of momentum in the x-direction, find the struck ball's x-component of momentum.3. Calculate the y-component of the first ball's final momentum after the collision in kg*m/s.4. Using the conservation of momentum in the y-direction, find the struck ball's y-component of momentum.

Answer 1

We are given the following situation:

Ball 1 strikes ball 2 and after the collision forms an angle of 30 degrees. To determine the x-component of the final momentum of the first ball we use the following formula:

`P_(1fx)=m_1v_(1f)\cos\theta_1`

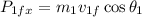
Where:

`\begin{gathered} P_(1fx)=final\text{ x-component of the momentum of ball 1} \\ m_1=\text{ mass of ball 1} \\ v_(1f)=\text{ final velocity of ball 1} \\ \theta_1=\text{ angle of ball 1} \end{gathered}`

Now, we substitute the values:

`P_(1fx)=(0.71kg)(2.17(m)/(s))\cos(30)`

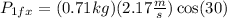
Solving the operations we get:

`P_(1fx)=1.33kg(m)/(s)`

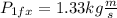
Therefore, the x-components of the momentum of the first ball is 1.33 kgm/s.

Part 2. To determine the x-component of the second ball we will do a balance of momentum in the x-direction:

`P_(10x)+P_(20x)=P_(1fx)+P_(2fx)`

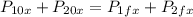
Where:

`\begin{gathered} P_(10x),P_(20x)=\text{ initial momentum in the x-direction of ball 1 and 2} \\ P_(2fx),P_(20x)=\text{ final momentum in the x-direction of ball 1 and 2} \end{gathered}`

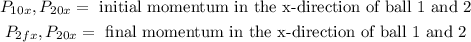
Since the second ball starts from rest we have that its initial momentum is zero, therefore:

`P_(10x)=P_(1fx)+P_(2fx)`

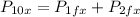
Now, we solve for the x-component of the momentum of the second ball:

`P_(10x)-P_(1fx)=P_(2fx)`

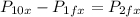
The initial momentum of the first ball is the product of its mass and velocity:

`m_1v_(01)-P_(1fx)=P_(2fx)`

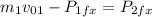
Now, we plug in the values:

`(0.71kg)(2.5(m)/(s))-1.33kg(m)/(s)=P_(2fx)`

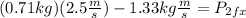
Solving the operations:

`0.44kg(m)/(s)=P_(2fx)`

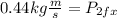
Part 3. To calculate the y-component of the first ball after the collision we will use the following formula:

`P_(1fy)=m_1v_(1f)\sin\theta`

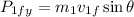
Now, we plug in the values:

`P_(1fy)=(0.71kg)(2.17(m)/(s))\sin(30)`

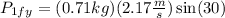
Solving the operations we get:

`P_(1fy)=0.77kg(m)/(s)`

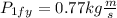
Therefore, the y-component of the momentum of the first ball is 0.77 kgm/s.

Part 4. To determine the y-component of the second ball we use a balance of momentum of the y-components of the balls:

`P_(10y)+P_(20y)=P_(1fy)+P_(2fy)`

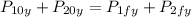
Since the first ball is not moving in the y-direction this means that its y-component of the momentum is 0. Since ball 2 is not moving initially this means that its momentum in the y-direction is zero.

`0=P_(1fy)+P_(2fy)`

Now we solve for the y-component of the second ball, and we get:

`-P_(1fy)=P_(2fy)`

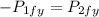
Therefore, the y-component of the second ball is:

`-0.77kg(m)/(s)=P_(2fy)`

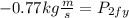
Therefore, the y-component of the second ball is -0.77 kgm/s.