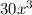Question

Find the GCF if the following terms . (30x^5 ,60x^3)

Answer 1

The coefficient of the GCF of a set of algebraic terms, wil be the GCF of the coefficients of the terms.

Notice that the coefficients in this case, are 30 and 60.

The greatest comon factor of this set, is 30, since:

`\begin{gathered} 30=30\cdot1 \\ 60=30\cdot2 \end{gathered}`

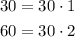
On the other hand, the variable x appears with an exponent of 5 in one case and an exponent of 3 in the other case. The greatest common factor for the variable x will be the lowest power, in this case, 3. Notice that:

`\begin{gathered} x^3=x^3\cdot1 \\ x^5=x^3\cdot x^2 \end{gathered}`

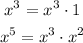
Then, we can factor out the following:

`30x^3`

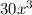
Notice that each term can be written as a product of this factor:

`\begin{gathered} 30x^5=30x^3(x^2)^{}^{}^{}_{} \\ 60x^3=30x^3(2)^{}_{} \end{gathered}`

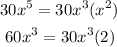
Therefore, the greatest common factor (GCF) is:

`30x^3`