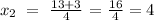Question

Find all real values of x such that f(x)=0 for f(x) = 2x^2 + 3x – 20

Answer 1

Consider first the general case of the equation

`ax^2+bx+c\text{ =0}`

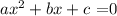
The general formula that solves this problem is given by

`x\text{ = }\frac{-b\text{ }\pm\sqrt[]{b^2-4ac}}{2a}`

In this case, the number of real solutions depends on the value that is inside the square root. For it to have a real value, it must happen that

`b^2-4ac\ge0`

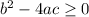
So first, let's check if this is our case. In our case a = 2, b = 3 and c = -20.

Then

`b^2-4ac=(3)^2-4\cdot2\cdot(-20)\text{ = 9 +160 = }169\ge0`

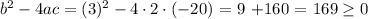
So in this case, the equation has real values. Now, recall that

`169=13^2`

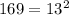
So our general solution becomes

`x\text{ = }\frac{-3\pm\sqrt[]{13^2}}{2\cdot2}`

Then,

`x\text{ = }\frac{-3\text{ }\pm\text{ 13}}{4}`

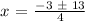
The symbol in the middle means that we get one different solution whenever we take either the plus sign of the minus sign. So the first solution would be

`x_{1\text{ }}=(13-3)/(4)\text{ = }(10)/(4)\text{ = }(5)/(2)`

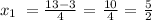
And the other solution would be

`x_{2\text{ }}=\text{ }(13+3)/(4)\text{ = }(16)/(4)=4`