Given data:
* The angle of the inclined plane is,
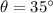
* The speed of the duck along the inclined plane is v = 5 m/s.
Solution:
The diagrammatic representation of the given case is,
From the triangle ABO,
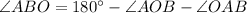
Substituting the known values,
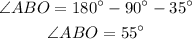
Thus, the inclined plane makes an angle of 55 degrees with the negative of the y-axis.
Similarly, the angle of the velocity of the duck along the inclined plane with the negative y-axis is 55 degrees.
Thus, the vertical component of the velocity is,
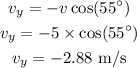
The horizontal component of the velocity is,
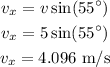
Thus, the horizontal component of velocity is 4.096 meters per second, and the vertical component of velocity is -2.88 meters per second.