Question

The height, h (in meters above ground), of a projectile at any time, t (in seconds), after the launch is defined by the function h(t) = −5t2 + 13t + 6. The graph of this function is shown below. When rounded to the nearest tenth, what is the maximum height reached by the projectile, how long did it take to reach its maximum height, and when did the projectile hit the ground?

Answer 1

As we can se from the graph, the maximum value of the function is almost 15 meters, it is reached between t=1s and t=2s, and the height is 0 again when the time is approximately 3 seconds.

We can find the exact values by using the equation.

First, find the zeroes of the function by setting h(t)=0 and solving the quadratic equation for t:

`\begin{gathered} h(t)=-5t^2+13t+6=0 \\ \Rightarrow t=\frac{-13\pm\sqrt[]{13^2-4(6)(-5)}}{2(-5)} \\ \Rightarrow t_1=-0.4;t_2=3 \end{gathered}`

Then, the projectile hits the ground at t=3s.

To find the time at which the projectile reaches its maximum height, find the average between both zeroes:

`t_(\max )=(t_1+t_2)/(2)=(-0.4s+3s)/(2)=1.3s`

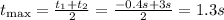
To find the maximum height, evaluate h at t=1.3s:

`h(1.3s)=-5(1.3)^2+13(1.3)+6=14.45`

Therefore, to the nearest tenth, the projectile reached a maximum height of 14.5 meters in 1.3 seconds and it took 3.0 seconds for it to hit the ground.

The correct option is the second one.