Question

Cos(theta) = - 3/4 and is in the 3rd quadrant, find the following:

Answer 1

`\begin{gathered} sin(\theta)=(-√(7))/(4) \\ cos(\theta)=-(3)/(4) \\ tan(\theta)=(√(7))/(3) \\ csc(\theta)=-(4)/(√(7)) \\ sec(\theta)=-(4)/(3) \\ cot(\theta)=(3)/(√(7)) \end{gathered}`

Explanation:

If theta is in the third quadrant, draw the diagram to easily identify the other trigonometric relations:

Solve for the missing leg of the triangle, using the Pythagorean theorem:

`\begin{gathered} \text{ adjacent}^2+\text{ opposite}^2=\text{ hypotenuse}^2 \\ -3^2+\text{ opposite}^2=4^2 \\ \text{ opposite=}√(16-9) \\ \text{ opposite=}√(7) \end{gathered}`

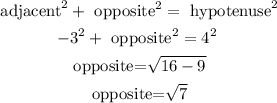
Therefore, for the trigonometric relationships:

`\begin{gathered} \text{ sin\lparen}\theta)=(opposite)/(hypotenuse) \\ \text{ cos\lparen}\theta)=(adjacent)/(hypotenuse) \\ tan(\theta)=(opposite)/(adjacent) \\ csc(\theta)=(hypotenuse)/(opposite) \\ sec(\theta)=(hypotenuse)/(adjacent) \\ cot(\theta)=(adjacent)/(opposite) \end{gathered}`

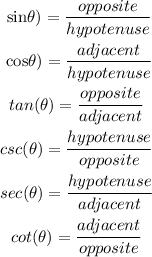
Now, substitute and solve for the relations:

`\begin{gathered} sin(\theta)=(-√(7))/(4) \\ cos(\theta)=-(3)/(4) \\ tan(\theta)=(√(7))/(3) \\ csc(\theta)=-(4)/(√(7)) \\ sec(\theta)=-(4)/(3) \\ cot(\theta)=(3)/(√(7)) \end{gathered}`