We have that
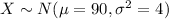
The parts the will be rejected when it's above 95 or when it's under 85, if we plot the normal distribution it would be
Then, the percentage of the parts that will be rejected corresponds to the area in blue, then, we must calculate the area under the normal distribution for
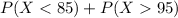
The normal distribution is symmetrical, then calculate P(X < 85) is the same as P(X > 95), then we write it as
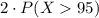
Calculate that integral is very hard, then, we must transform that in a standard normal X ~ N(0, 1) and use a table to find the result, to do that we must write a value z, it's a transformation to take a value on our normal and leads it to the standard normal, it's
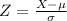
We have X = 95, μ = 90 and σ = 2
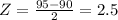
Then 2.5 is the value we are going to search in our table, using the complementary cumulative table for 2.5 we get 0.00621, which means
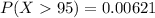
And the total percentage will be
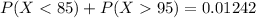
We can write it in percentage
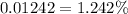
Therefore, only 1.24% will be rejected.
It's a very low value, but it's expected because it's more than 2 standard deviations (95%).