Question

The number of bacteria in a certain population increases according to a continuous exponential growth model, with a growth rate parameter of 4.3% per hour. How many hours does it take for the size of the sample to double? Note this is a continuous exponential growth model. Do not round any intermediate computations, and round your answer to the nearest hundredth.

Answer 1

16.12 hours

Explanation:

A continuous exponential growth model is given below:

`P(t)=P_oe^(rt)`

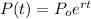
• The growth rate, r = 4.3% = 0.043

,

• t = time in hours

,

• Po = Initial population

,

• P(t) = Present population

We want to find the number of hours it takes the population to double. That is if the initial population, Po = 1

• The present population, P(t) = 1 x 2 = 2.

Substitute these values into the model above to get:

`2=1(e^(0.043t))`

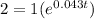
Since natural logarithm(ln) is the inverse of exponential, take the natural logarithm of both sides to remove the exponential operator.

`\begin{gathered} \ln (2)=\ln (e^(0.043t)) \\ \ln (2)=0.043t \end{gathered}`

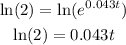
Divide both sides by 0.043.

`\begin{gathered} (\ln (2))/(0.043)=(0.043t)/(0.043) \\ t=(\ln(2))/(0.043) \\ t\approx16.12 \end{gathered}`

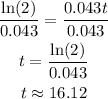
It will take 16.12 hours for the size of the sample to double.