Answer:
Part A) 10 meters
Part B) 24 meters
Explanation:
We are going to be using the Pythagorean Theorem, that applies exclusively to right triangles:
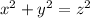
By counting the bottom and left sides of the triangle, we know that the length is 6, and 8 meters respectively.
Now, apply the Pythagorean Theorem to find the Hypotenuse:
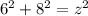
Simplify:
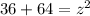
Add:
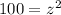
Take the Square Root of Both Sides:
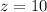
Now, we know that the distances from the starting point to Obstacle 2 is 10 meters (Part A)
To solve Part B, simply add the length of all 3 sides
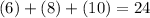
The length of the entire course is 24 meters (Part B)