Let's plot the function that represents. The simplest way is to calculate points every certain value and then place them on the plane.
As we can see in the graph there are two asymptotes. A vertical asymptote for x = -4. A horizontal asymptote for y = 0.
Now let's calculate the asymptotes analytically.
To do this we must factor and simplify our expressions. As you can see the denominator expression is a trinomial that can be simplified/factored.
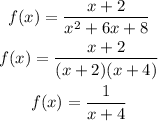
As we can see in the simplification when x = -4 the denominator is 0 and this is where our vertical asymptote appears.
On the other hand, to see our horizontal asymptote we evaluate the limit of the function when it tends to infinity. Therefore when x takes a very large value then f(x) is 0 and there appears our horizontal asymptote at y = 0.
The simplified function is as follows:
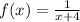
Now we will evaluate what happens when x tends to infinity
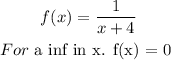
Evaluating points.
The simplest way to plot a curve is by point evaluation.
For example, let's evaluate x = 1
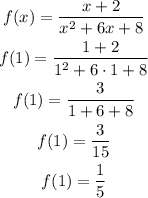
In this case the point would be (1,1/5)