We know that the mid point formula is
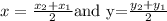
we will check one by one which option make this formula by substituing values given:-
It is given that
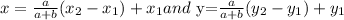
Now when a=1 anf b=2 we have
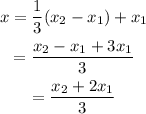
which is not the midpoint formula
Now let's substitute a=1 and a+b=2
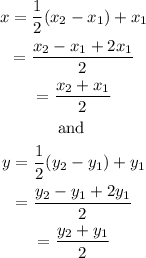
which is the required formula.
Hence the correct option is a=1 , a+b=2