Question

Suppose that y varies directly as the square root of x, and that y = 49 when x = 49. What is y when x = 128? Round your answer to two decimal places if necessary

Answer 1

Since y varies directly with square root x, so

`y=k√(x)`

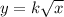
k is the constant of variation

We will find it using the initial values of x and y

Since the initial values are:

y = 49

x = 49

Substitute them in the rule to find k

`\begin{gathered} 49=k√(49) \\ 49=k(7) \\ 49=7k \\ (49)/(7)=(7k)/(7) \\ 7=k \end{gathered}`

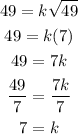
The value of k is 7, so the equation will be

`y=7√(x)`

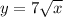
We need to find the value of y at x = 128, so

Substitute x in the rule by 128

`\begin{gathered} y=7√(128) \\ y=56√(2)=79.1959595 \end{gathered}`

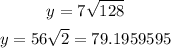
Round it to two decimal places, so

y = 79.20